Diffusion이나 Generative Model은 데이터의 Distribution을 추청하고 샘플링한다. 그렇다면, 이미지가 ‘확률분포’라는 말은 무슨말일까? Naive하게 감이 오는 것 같지만, 이 점을 정확히 짚고 넘어가자.
How Generative Model Works
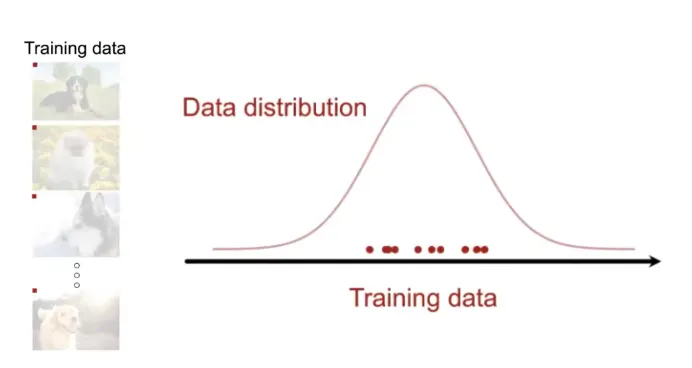
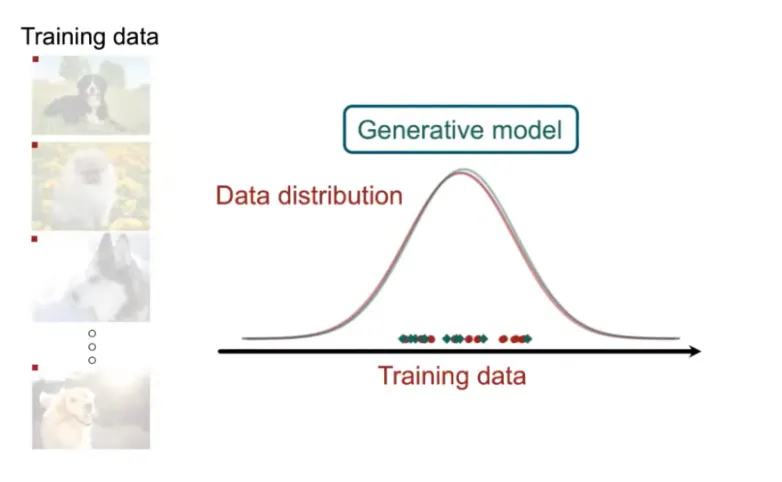
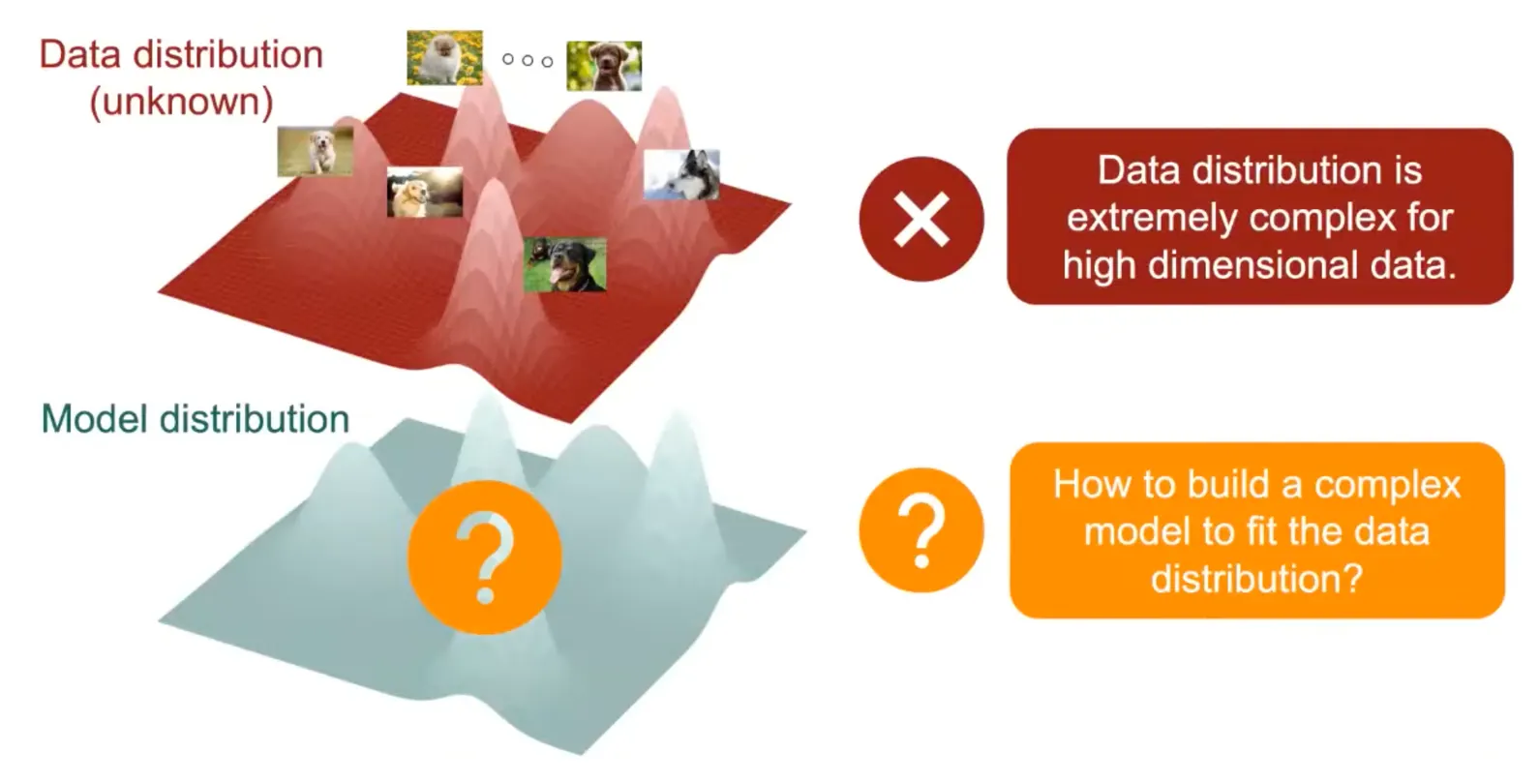
먼저, 좌측과 같은 강아지 이미지들이 있다고 할 때, 이 Data의 Distribution은 붉은색 선과 같다고 볼 수 있다.
여기서 문제는 ‘실제 데이터의 Distribution’을 알아낼 수 있는 방법이 없다는 것이다.
따라서 모델을 이용하여 이 Data의 Distribution을 추정하게 된다. (푸른색 선)
그리고 이렇게 추정된 Distribution을 통하여 샘플링을 하면 실제 데이터와 유사한 이미지를 생성할 수 있는 것이다. (푸른색 점)
우리는 이것을 Generative Model이라고 한다.
The challenge of modern generative models
그렇다면 여기서 질문이 생긴다.
‘이미지’의 ‘확률분포’라는 것은 무슨 의미일까?
‘이미지’가 High-dimensional data 라는 말은 무슨 의미일까?
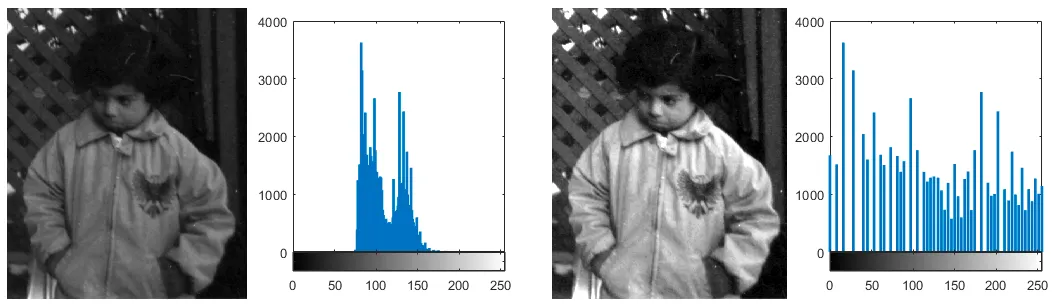
위와 같은 강아지 사진을 보자.
각각의 픽셀은 0~255의 값을 가지는 RGB 픽셀이다.
즉 [0,0,0] 부터 [255,255,255] 까지 16,581,375개의 값을 가질 수 있다.
이를 1차원 Distribution 으로 나타낼 수 있다.
히스토그램을 생각하면 이해가 빠르다.
첫번째 픽셀을 보자.
수많은 강아지 사진에서 왼쪽 상단의 픽셀은 보통 ‘하늘’에 해당할 것이고,
많은 사진들이 낮의 하늘색과 밤의 검은색에 몰려있을 것이다.
그렇다면 오른쪽과 같은 distribution 을 가진다고 생각해볼 수 있다.
이제 두번째 픽셀을 보자.
첫번째 픽셀에 conditioned된 두번째 픽셀의 distribution 는 파란색 선과 같이 나타낼 수 있을 것이다.
이제 두 픽셀의 joint distribution 는 좀 더 복잡한데,
오른쪽과 같이 2차원의 그래프로 나타낼 수 있다.
같은 방식으로 세번째 픽셀을 고려한다면, joint distribution은 다음과 같다.
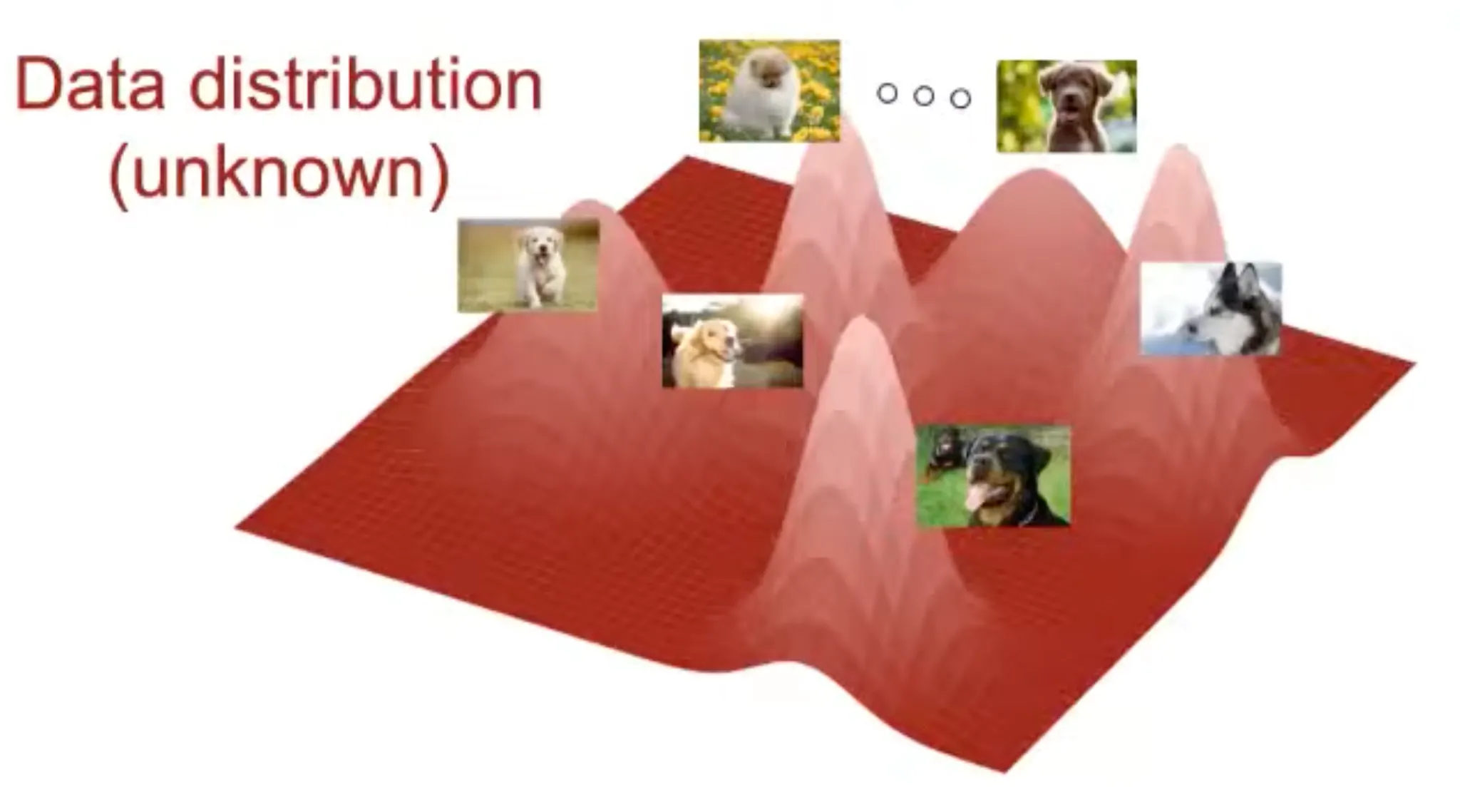
이런식으로 pixel의 개수를 늘려나가면 이미지의 distribution은 굉장히 복잡해진다.
The complexity of the data distribution grows very quickly.
px 이미지의 경우 65,025 차원을 가지게 되는데, 이를 시각화 하면 다음과 같다.
이미지나 비디오는 데이터 분포가 매우 고차원이고, 실제로 이 분포를 알아낼 수도 없다.
이것은 생성모델이 극복해야 할 큰 난관이다.
Data distribution is extremly complex for high dimensional data.
따라서 모델을 통해서 데이터의 분포를 추정 (fit) 해야 한다.
이것이 Diffusion Model, GAN을 비롯한 Generative Model의 목표이다.
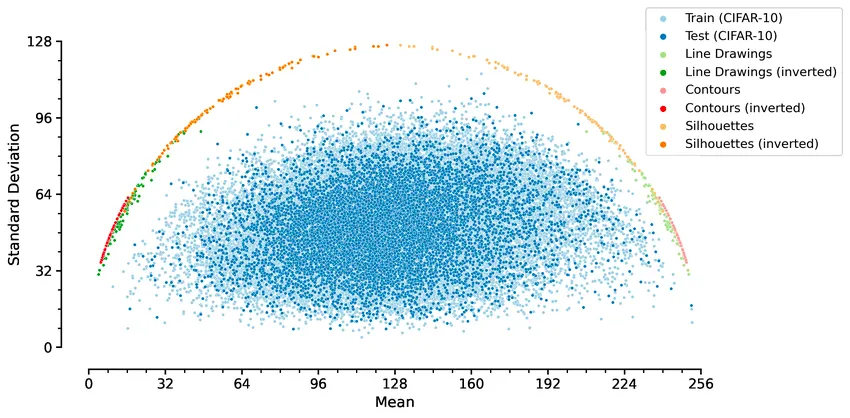
Real Dataset Distribution
Credit: Biological convolutions improve DNN robustness to noise and generalisation
위 그림은 Real-Dataset인 Cifar-10의 Statistics를 Plot한 것이다.
특히 Line, Silhouette 이미지들은 위 수식에 따라 원을 그리는 흥미로운 plot을 보인다.
이는 이미지를 로 Normalize 했을 때, 인 관계를 볼 수 있다.
Build a complex model
그렇다면 어떻게 복잡한 모델을 만들 수 있을까?
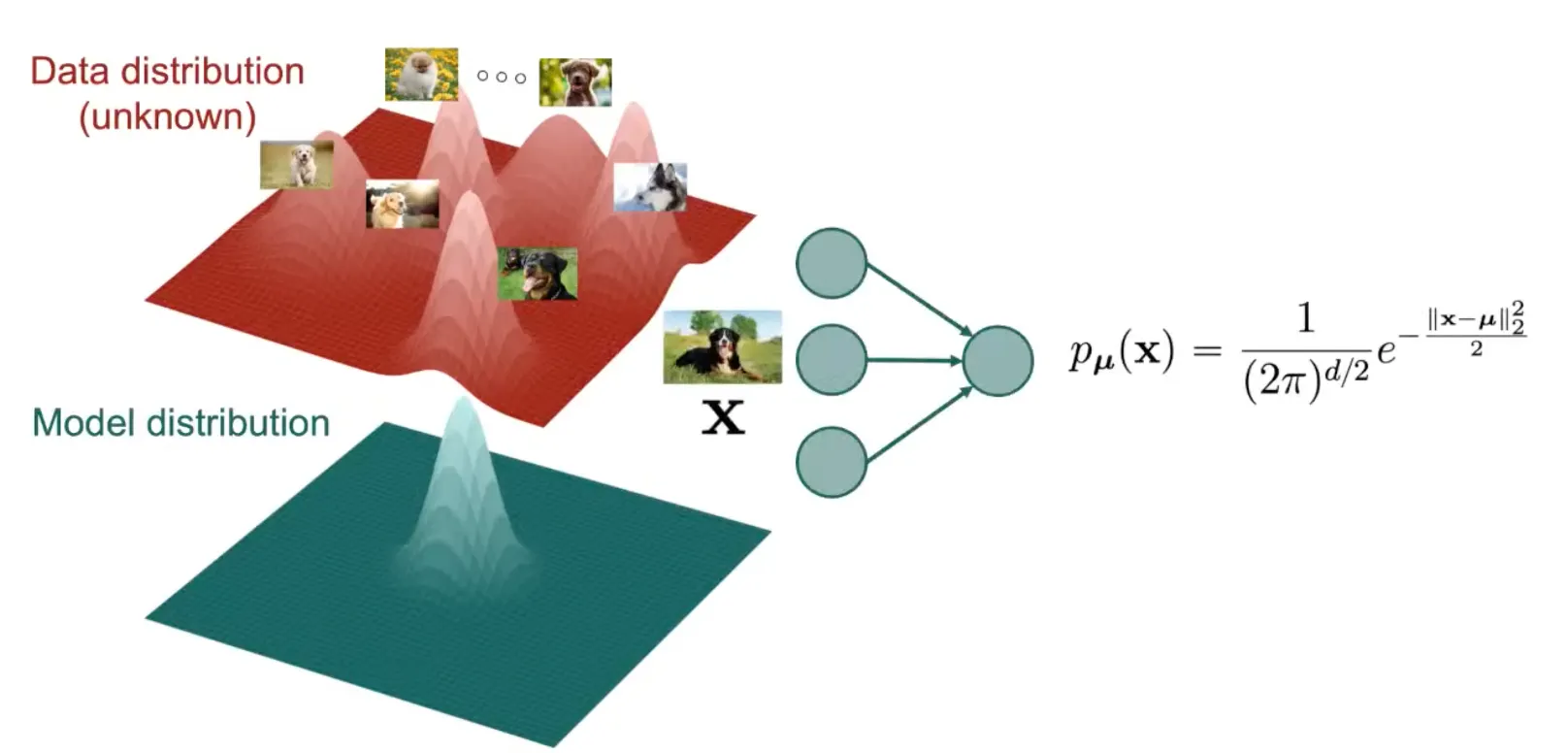
가장 Naive한 방법은 가우시안으로부터 시작하는 것이다.
Gaussian Model은 input 를 exponentional 지수로 취하고, 상수로 나누어 data point의 probability를 간단한 방법으로 예측한다.
하지만 Gaussian은 너무 간단해서 매우 복잡한 data distribution을 추정하기에 충분하지 않다.
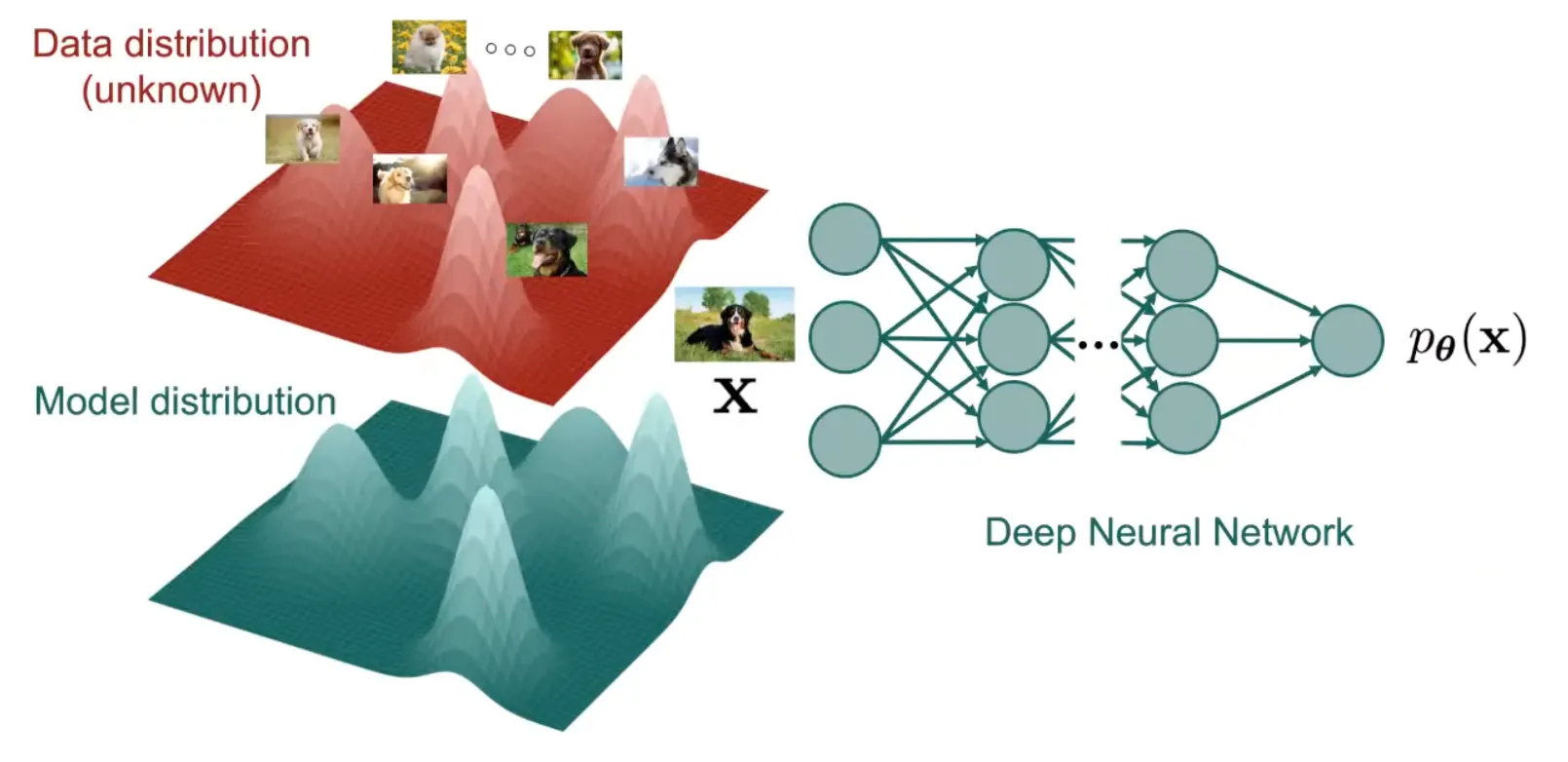
이를 위해서 더 많은 gaussian을 추가해 Deep Neural Netwrok을 사용할 수 있지만, 이 역시 충분하지 않다.
따라서 Deep Generative Models의 목표는 더욱 복잡한 모델을 도입하여 데이터의 분포를 효과적으로 추정하는 것이다.
하지만 실제로 이러한 모델을 만드는 것은 어렵다.
왜냐하면 모든 확률의 합은 1이 되어야 한다는 강력한 제약사항 (restriction)이 존재하기 때문이다.
따라서 Network가 어떤 확률분포를 추정하되 총 합이 1이 되어야 한다는 것은 굉장히 중요한 과제이다.
Score-based Diffusion Model
그렇다면 어떻게 이 제약사항을 극복할 수 있을까?
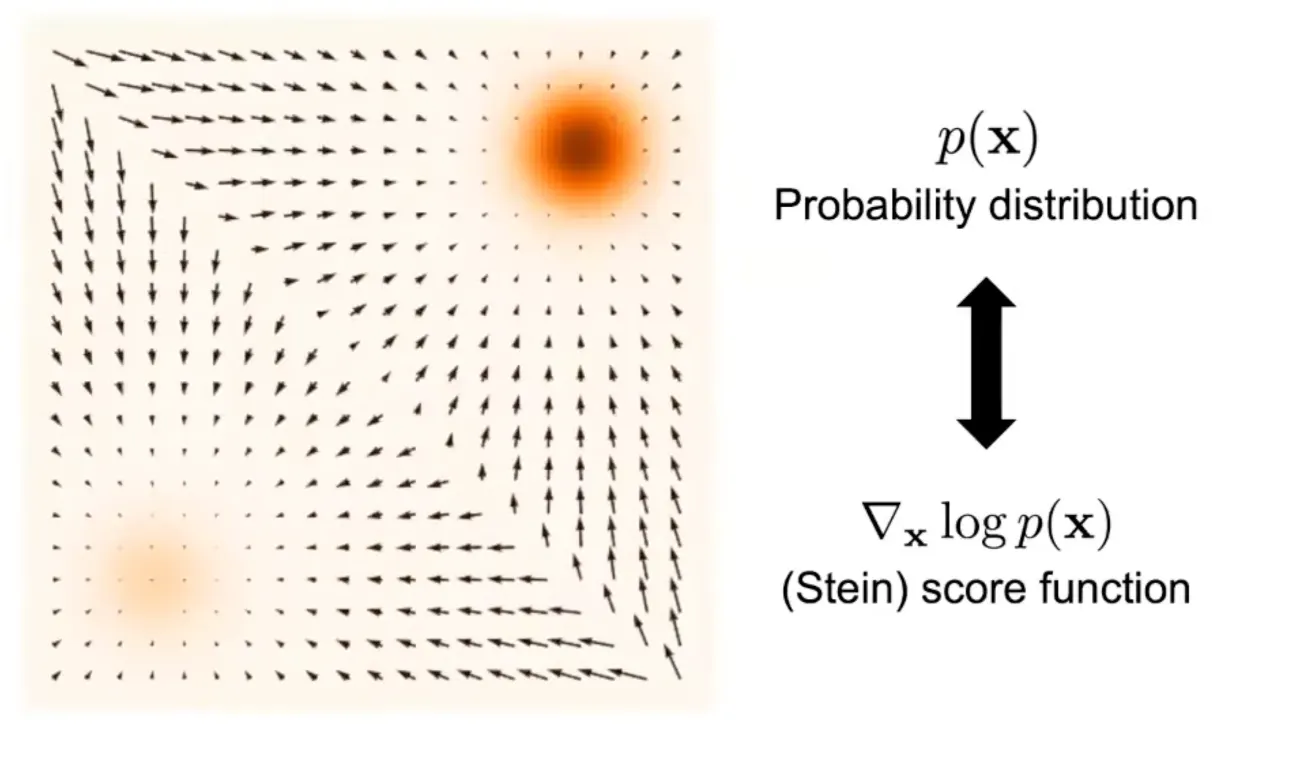
Y. Song은 score function을 이용해 이를 극복했다.
score-function는 probability의 log derivative이다.
즉 분포의 방향을 가르키는 벡터장 (Field)이다.
이 score function을 사용한다면 더이상 총 합이 1이 되어야 한다는 강력한 제약사항에서 벗어날 수 있고
score function을 통해 probability distribution을 추정할 수 있다.
이러한 컨셉은 전기장과 포텐셜의 관계와 매우 유사하다.
Potential은 스칼라로써, 전위 값을 가진다.
Field은 벡터장으로써, 포텐셜이 가장 빠르게 감소하는 방향을 가리킨다.
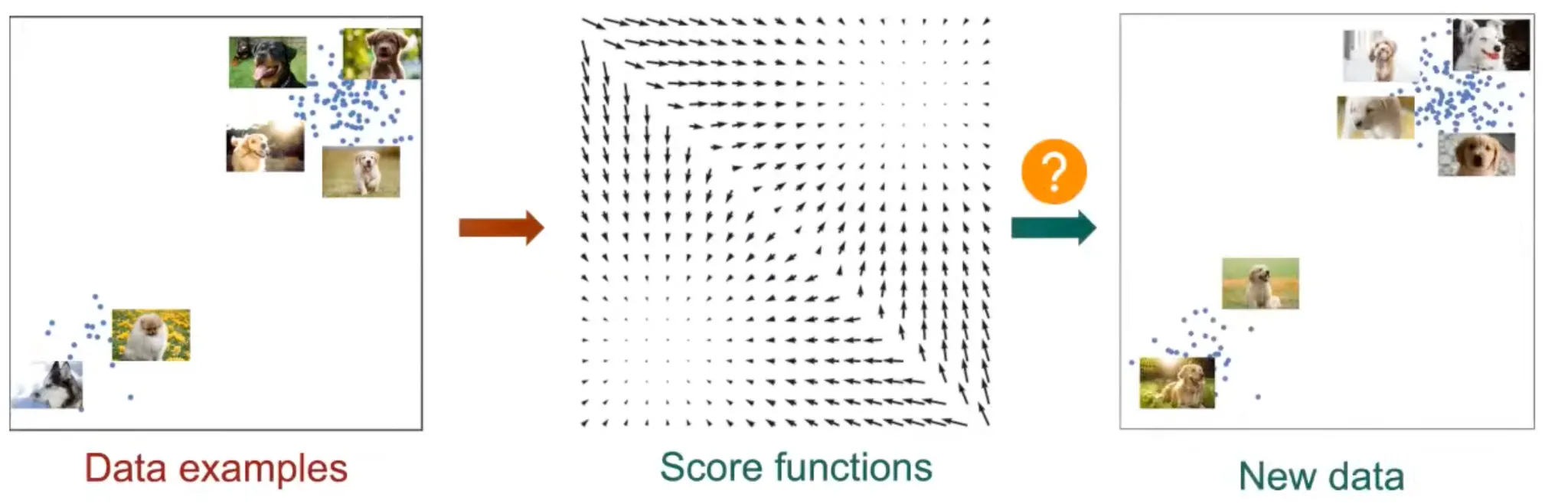
그렇다면 score function으로 genrative modeling을 설명해보자.
1.
large dataset을 수집한다.
2.
Network로 score function을 추정한다.
probability 를 추정하지 않으므로 제약사항이 없어서 모델링하기 매우 간단하다는 장점이 있다.
3.
이러한 score function으로부터 새로운 data를 샘플링 할 수 있다.
이미지를 distribution으로 표현하는 것과 score based diffusion의 아이디어까지 간단하게 알아봤다.
더욱 자세한 내용은 다음 컨텐츠를 참고하기 바란다.